

Remember that when you are manually graphing logarithmic functions, x values of. Internet Explorer is not recommended for this applet. Then, plot the points onto the graph, followed by connecting the dots. If you are having trouble viewing the applet, be sure JavaScript is enabled in your browser. No other libraries/dependencies are required. This applet was created using JavaScript and HTML Canvas.
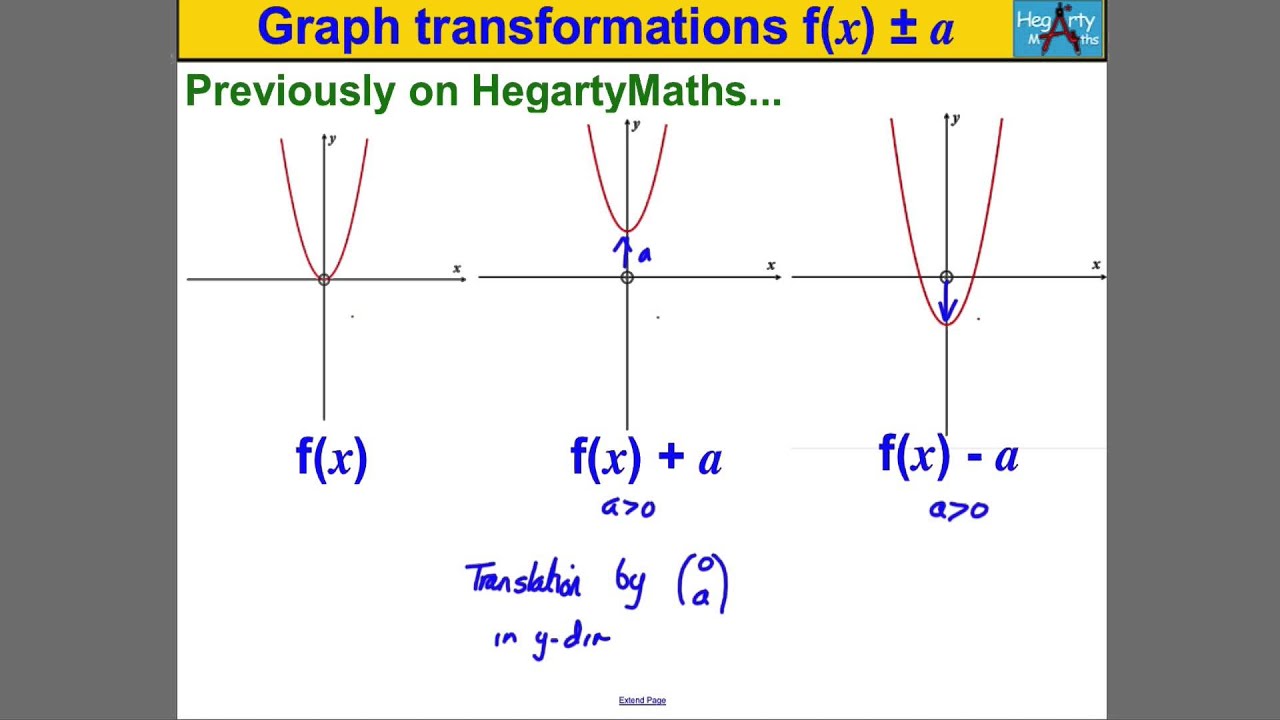
If D is positive, the graph will shift up by a factor of D if D is negative, the graph will shift down.Īny combination of these transformations can be applied to a function simultaneously, as demonstrated in this applet. When C is negative, the graph will shift to the left.Īdding a value D to a trig function will translate its graph vertically. When C is positive, the graph will appear to shift to the right. The phase shift of a trigonometric function is calculated using the formula A phase shift results from adding a value to the variable before the evaluating the function. The phase shift of a trigonometric function refers to its horizontal shift to the right. When |B| is less than 1, the period is larger than the original, and the function will appear stretched. When |B| is larger than one, the new period is smaller than the original, so the function will appear horizontally compressed. By altering the value of B (the multiplier of the variable before the function is evaluated), we can change the period of the function according to the formula sin(x), cos(x), sec(x), and csc(x) all have a period of \(2\pi\), while tan(x) and cot(x) have a period of \(\pi\). The period of any trig function is the length of one cycle. Note that a negative value of A will flip the graph of any function across the \(x\)-axis. The other trig functions (tangent, cotangent, secant, and cosecant) do not have an amplitude, but multiplication by A will affect their steepness. We can change the amplitude of these functions by multiplying the function by a constant A. This pre-image in the first function shows the function f(x) x 2. The amplitude of a sinusoidal trig function (sine or cosine) is it's 'height,' the distance from the average value of the curve to its maximum (or minimum) value. We can apply the transformation rules to graphs of quadratic functions. The graphs of the six basic trigonometric functions can be transformed by adjusting their amplitude, period, phase shift, and vertical shift. Graph transformations examples Example 1: applying a translation in the y- direction The diagram shows the graph of yf (x) y f (x) and a point on the graph P (2,5). Use the slider to zoom in or out on the graph, and drag to reposition. The original base function will be drawn in grey, and the transformation in blue. A function presented in tabular form can also be reflected by multiplying the values in the input and output rows or columns accordingly.Choose a base trigonometric function, then change its amplitude, period, phase shift, and vertical shift using the inputs.The order in which the reflections are applied does not affect the final graph. A graph can be reflected both vertically and horizontally.A graph can be reflected horizontally by multiplying the input by –1. A non-rigid transformation58 changes the size and/or shape of the graph. A rigid transformation57 changes the location of the function in a coordinate plane, but leaves the size and shape of the graph unchanged. We input a value that is 3 larger for g\left(x\right) because the function takes 3 away before evaluating the function f. When the graph of a function is changed in appearance and/or location we call it a transformation. To get the same output from the function g, we will need an input value that is 3 larger. For example, we know that f\left(2\right)=1. The formula f\left(x\right)=f\left(x - 3\right) tells us that the output values of g are the same as the output value of f when the input value is 3 less than the original value.


 0 kommentar(er)
0 kommentar(er)
